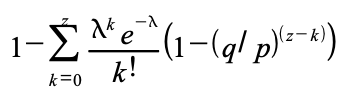Dürüst zincir ile bir saldırgan zinciri arasındaki yarış Binom Rastgele Yürüyüşü olarak nitelendirilebilir. Başarılı olma durumu dürüst zincirin bir blok uzatılarak öncülüğünü 1 arttırması, başarısızlık durumu ise saldırganın zincirinin bir blok uzatılarak aralığın 1 azalmasıdır.

Bir saldırganın belirli bir açığı yakalama olasılığı Kumarbazın İflası problemine benzemektedir. Sınırsız krediye sahip bir kumarbazın oyuna borçla başladığını ve başabaş noktasına gelebilmek için sonsuz sayıda deneme oyunu oynadığını varsayın. Başabaş noktasına ulaşabilme olasılığını veya saldırganın dürüst zinciri yakalayabilme olasılığını şu şekilde hesaplayabiliriz [8]:

p = dürüst bir düğümün sonraki bloğu bulma olasılığı
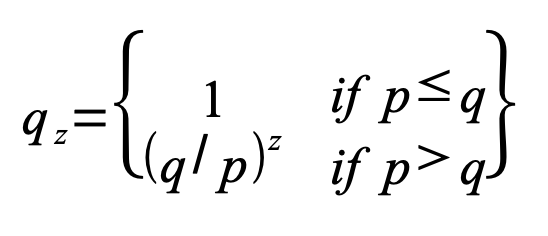
q = saldırganın bir sonraki bloğu bulma olasılığı
q _z = saldırganın z blok geriden gelip yakalama ihtimali

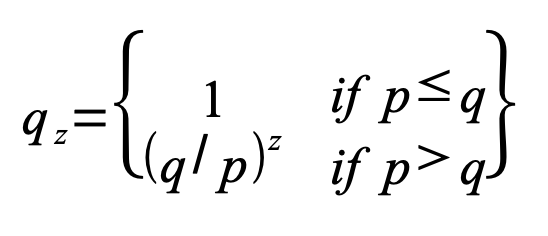
P > q varsayımımıza göre, saldırganın yakalaması gereken blok sayısı arttıkça, olasılık katlanarak düşmektedir. Bütün olanaksızlıklarla beraber, saldırgan başlarda eğer bir dizi şanslı hamle yapmazsa, kazanma ihtimali zincirin gerisinde kaldıkça hızla azalmaktadır.

Şimdi yeni bir işlemdeki alıcının, gönderenin işlemi değiştiremeyeceğinden yeterince emin olmadan önce ne kadar beklemesi gerektiğini ele almaktayız. Gönderenin, alıcıyı belli bir süre için kendisine ödeme yaptığına inandırmak isteyen, belli bir zaman geçtikten sonra ise ödemeyi kendisine geri döndürmek isteyen bir saldırgan olduğunu varsaymaktayız. Bu olduğunda alıcı uyarılacaktır ancak gönderen bunun için artık çok geç olacağını ümit etmektedir.

Alıcı yeni bir anahtar çifti oluşturur ve imzalamadan kısa bir süre önce gönderene açık anahtarı verir. Bu, gönderenin önceden sürekli olarak üstünde çalışarak, bloklardan oluşan bir zinciri hazırlamasını ve bu zincirin öne geçtiği şanslı bir anda işlemi çalıştırmasını önlemektedir. İşlem gönderildikten sonra dürüst olmayan gönderici, işleminin alternatif bir versiyonunu içeren paralel bir zincir üzerinde gizlice çalışmaya başlar.

Alıcı, işlem bir bloğa eklenene ve bunun arkasına z kadar blok bağlanana kadar bekler. Saldırganın ne kadar ilerleme kaydettiğini tam olarak bilmez ancak dürüst blokların blok başına beklenen ortalama bir süre aldığını varsayarsak, saldırganın yaptığı potansiyel ilerleme beklenen değerli bir Poisson dağılımı olacaktır:

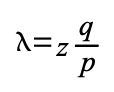
Saldırganın herşeye rağmen yetişebilme ihtimalini elde etmek için, o noktadan zinciri yakalayabilme olasılığı ile elde edebileceği her ilerleme için Poisson yoğunluğunu çarparız:

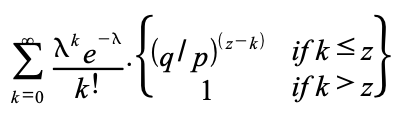
Sonsuz dağılım kuyruk toplamını almaktan kaçınmak için yeniden düzenliyoruz...