10. Privacy
The traditional banking model achieves a level of privacy by
limiting access to information to the parties involved and the
trusted third party. The necessity to announce all transactions
publicly precludes this method, but privacy can still be
maintained by breaking the flow of information in another place:
by keeping public keys anonymous. The public can see that someone
is sending an amount to someone else, but without information
linking the transaction to anyone. This is similar to the level of
information released by stock exchanges, where the time and size
of individual trades, the "tape", is made public, but without
telling who the parties were.
As an additional firewall, a new key pair should be used for each
transaction to keep them from being linked to a common owner. Some
linking is still unavoidable with multi-input transactions, which
necessarily reveal that their inputs were owned by the same owner.
The risk is that if the owner of a key is revealed, linking could
reveal other transactions that belonged to the same owner.
11. Calculations
We consider the scenario of an attacker trying to generate an
alternate chain faster than the honest chain. Even if this is
accomplished, it does not throw the system open to arbitrary
changes, such as creating value out of thin air or taking money
that never belonged to the attacker. Nodes are not going to accept
an invalid transaction as payment, and honest nodes will never
accept a block containing them. An attacker can only try to change
one of his own transactions to take back money he recently spent.
The race between the honest chain and an attacker chain can be
characterized as a Binomial Random Walk. The success event is the
honest chain being extended by one block, increasing its lead by
+1, and the failure event is the attacker's chain being extended
by one block, reducing the gap by -1.
The probability of an attacker catching up from a given deficit is
analogous to a Gambler's Ruin problem. Suppose a gambler with
unlimited credit starts at a deficit and plays potentially an
infinite number of trials to try to reach breakeven. We can
calculate the probability he ever reaches breakeven, or that an
attacker ever catches up with the honest chain, as follows [8]:
p = probability an honest node finds the next block
q = probability the attacker finds the next block
q z = probability the attacker will ever catch up from z blocks behind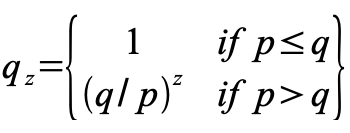
q = probability the attacker finds the next block
q z = probability the attacker will ever catch up from z blocks behind